構造方程式モデリングとは
人間の認知には、ときに因果的な関係を誤って認識してしまう傾向があります。この因果関係の錯覚と呼ばれる認知バイアスは、複雑な現象を単純化して理解しようとする際に生じやすく、意思決定や判断に悪影響を及ぼす可能性があります。この認知バイアスに対抗する有効な手段の一つとして、今回取り上げる「構造方程式モデリング」(SEM:Structural Equation Modeling)があります。
SEMは、重回帰分析と同様、広く活用されてきた手法で、複数の変数間の因果関係を探究し、理論的枠組みをデータに基づいて検証するのに役立ちます。この手法は、単純な回帰分析を超えて、複雑な変数の相互作用と潜在変数の関係をモデル化する能力を持ちます。
概念と適用範囲
SEMは、潜在変数を含む複数の変数間の関係性を解析します。この手法は、観測されたデータから因果的な構造を評価し、変数間の直接的および間接的な関係性に迫れることから、心理学、教育学、マーケティングなど、様々な社会科学の領域で使われています。特に、複雑な因果関係のモデル化、潜在変数の分析、理論的仮説の検証に有効です。
基本的な手順
ステップ❶:理論モデルの構築
分析の出発点は、分析者が理論や先行研究に基づき構築した変数間の関係性を表す理論モデルです。このモデルは、観測変数間の関係、観測変数の背後にあると考えられる潜在変数間の関係、および観測変数と潜在変数の関係を表す因果パスで表現されます。
ステップ❷:統計モデルの定式化
理論モデルを統計的に表現可能な形式に変換します。この過程では、測定モデルと構造モデルと呼ばれる2つのモデルが登場し、測定モデルでは、潜在変数とそれを測定する観測変数の関係性が定義されます。例えば、「学習意欲」という潜在変数は、「授業への出席率」や「宿題の提出率」といった観測変数で測定されるだろうといった具合です。
- 測定モデル:潜在変数が、観測変数によってどのように測定されるかを表す。
- 構造モデル:主に、潜在変数間の因果的な関係性を表す。
もう一つの構造モデルでは、主に潜在変数間の因果的関係が定義されます。例えば「学習環境」という潜在変数が、「学習成果」という別の潜在変数に影響を与えるといった関係です。もちろん、理論モデル次第では、観測変数が直接的に他の潜在変数や観測変数に影響を与えるケースも、構造モデルに含めることができます。
ステップ❸:モデルの推定、評価、および解釈
収集したデータを用いてモデルのパラメータを推定し、モデルの適合度を評価します。このステージでは適合度指標を用いて、モデルがデータにどの程度良く適合しているかを判断します。モデルが十分にデータに適合していなければ理論モデルを再考し、十分であれば推定されたパラメータを用いて変数間の関係性を解釈します。
学生の学習成果のモデリング例
学生の学習成果を説明するモデルを構築する際、「学習環境」や「学習動機」といった潜在変数が、学生の「学習成果」に影響を与えると考えることができます。学習環境は、図書資源の充実度や教師の支援の質といった観測変数から測定できると仮定し、学習動機は、目標志向性や自己効力感、興味関心といった観測変数から測定できると仮定します。また、学習成果も単に試験の点数だけでは測れない概念であり、クラス参加度のような学習姿勢も含めた潜在変数として扱うこととします。
このような仮定のもと、ダミーデータの生成からモデル解釈の過程をサンプルコードを用いて例示します。ここでは説明を簡潔にするため、理論モデルを感覚的に扱いますが、実際の分析設計では、過去の研究知見に基づいて理論モデルの妥当性を十分に吟味し説明できることが大切です。
測定モデルの提示
- 潜在変数「学習成果」は、観測変数である「試験成績」、「課題提出率」、「クラス参加度」によって測定されると仮定します。
- 潜在変数「学習環境」は、観測変数である「図書資源」、「教師の支援」、「グループの活動性」によって測定されると仮定します。
- 潜在変数「学習動機」は、観測変数である「目標志向性」、「自己効力感」、「興味関心」によって測定されると仮定します。
構造モデルの提示
「学習環境」と「学習動機」という2つの潜在変数が「学習成果」という潜在変数に影響を与える構造を考えます。つまり、学習成果は、学習環境と学習動機の両方から影響を受けると仮定します。
ダミーデータの生成コード
Pythonを使用して、上記のモデルをベースとしたダミーデータを生成しておきます。
import numpy as np
import pandas as pd
np.random.seed(42)
n_samples = 500
学習環境 = np.random.normal(loc=0.0, scale=1.0, size=n_samples)
学習動機 = np.random.normal(loc=0.0, scale=1.0, size=n_samples)
学習成果 = 0.6 * 学習環境 + 0.4 * 学習動機 + np.random.normal(loc=0.0, scale=0.5, size=n_samples)
試験成績 = 0.7 * 学習成果 + np.random.normal(loc=0.0, scale=0.5, size=n_samples)
課題提出率 = 0.6 * 学習成果 + np.random.normal(loc=0.0, scale=0.5, size=n_samples)
クラス参加度 = 0.5 * 学習成果 + np.random.normal(loc=0.0, scale=0.5, size=n_samples)
図書資源 = 0.6 * 学習環境 + np.random.normal(loc=0.0, scale=0.5, size=n_samples)
教師の支援 = 0.7 * 学習環境 + np.random.normal(loc=0.0, scale=0.5, size=n_samples)
グループの活動性 = 0.5 * 学習環境 + np.random.normal(loc=0.0, scale=0.5, size=n_samples)
目標志向性 = 0.6 * 学習動機 + np.random.normal(loc=0.0, scale=0.5, size=n_samples)
自己効力感 = 0.7 * 学習動機 + np.random.normal(loc=0.0, scale=0.5, size=n_samples)
興味関心 = 0.5 * 学習動機 + np.random.normal(loc=0.0, scale=0.5, size=n_samples)
df = pd.DataFrame({
'試験成績': 試験成績,
'課題提出率': 課題提出率,
'クラス参加度': クラス参加度,
'図書資源': 図書資源,
'教師の支援': 教師の支援,
'グループの活動性': グループの活動性,
'目標志向性': 目標志向性,
'自己効力感': 自己効力感,
'興味関心': 興味関心
})
df.head()モデル推定のためのコード
SEMを扱う専用ライブラリsemopyを利用し、モデル推定の流れを示します。ここでのコードは、前述のダミーデータ生成に続く形で、実際に構造方程式モデルを定義し、生成データに適合させる流れになっています。
モデルの定義:学習環境は図書資源、教師の支援、グループの活動性によって、学習動機は目標志向性、自己効力感、興味関心によって。学習成果は試験成績、課題提出率、クラス参加度によって測定されると仮定しました。これらは測定モデルとして表現されます。最後に、学習環境と学習動機が学習成果に影響を与えるという仮定が構造モデルとして表されています。
from semopy import Model, Optimizer, calc_stats
model_desc = """
# 測定モデル
学習成果 =~ 試験成績 + 課題提出率 + クラス参加度
学習環境 =~ 図書資源 + 教師の支援 + グループの活動性
学習動機 =~ 目標志向性 + 自己効力感 + 興味関心
# 構造モデル
学習成果 ~ 学習環境 + 学習動機
"""モデルの推定:生成したダミーデータdfに対し、上記のモデルを適合させます。Modelクラスのインスタンスmodがもつfitメソッドを使用して、モデルパラメータを推定します。
mod = Model(model_desc)
res = mod.fit(df)結果の取得と解釈
モデルの適合度指標を取得し、モデルの当てはまり具合いを評価します。
stats = calc_stats(mod)
print(stats.T)例えば、GFI(Goodness of Fit Index)は、0以上1以下の値を取り、1に近いほどデータへの当てはまりが高いことを表します。AGFIは、GFIをモデルの自由度で調整したもので、モデルの複雑さを割り引いて評価する際に参照されます。今回は、データもモデルも同じ理論モデルに基づき作られているので、どちらも1.0に近い値になります。
モデルの適合度が十分に高いと評価できたら、semopyのinspectメソッドを使って、推定されたモデルのパラメータや統計量を確認します。
estimates = mod.inspect()
display(estimates)このコードは、学習環境や学習動機から学習成果への因果的な影響度、潜在変数である学習成果や学習環境などを測定する観測変数の因子負荷量の推定値などを提供します。これらの情報を用いて、理論モデルの変数間の関係性の強さを評価できます。
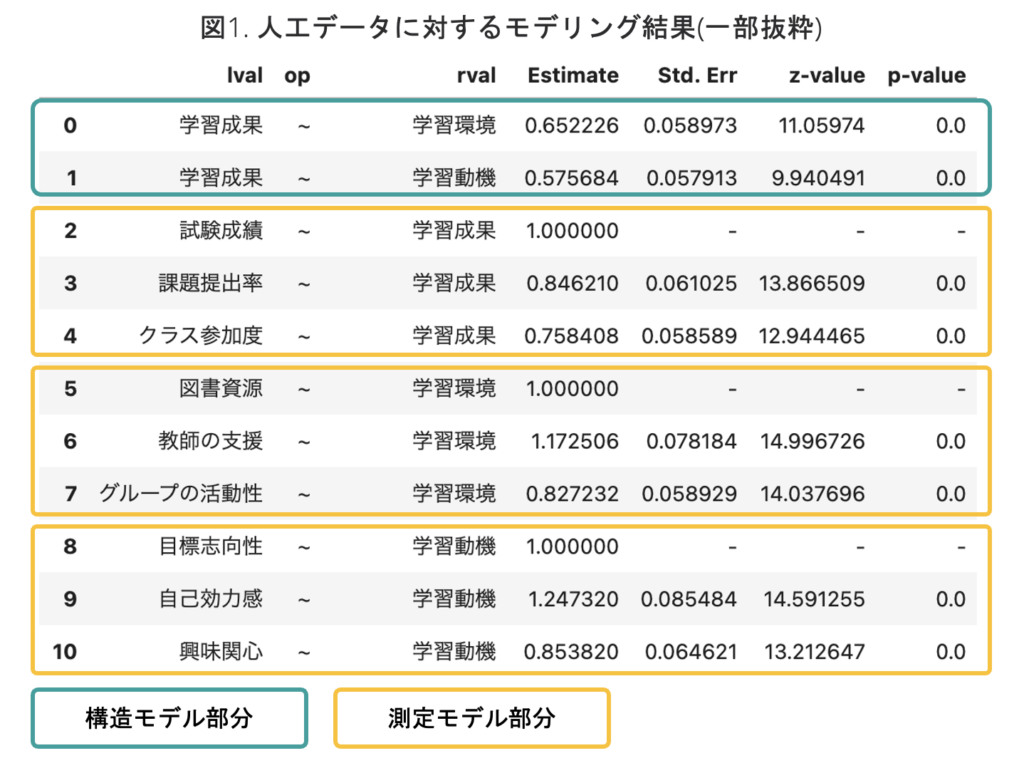
今回のように自身で生成したデータであれば、その推定結果も理解しやすいでしょう。ただ、上記結果はダミーデータの特徴をよく捉えていると思いますが、ノイズのscaleを大きくしたり、データサンプル数を減らしたりすると、必ずしも狙い通りの推定値にならないことは覚えておいて下さい。
より重要なことは、データ生成過程をさまざまに変化させた時のモデリング結果の変化をチェックする習慣です。この習慣が、データ分析結果の解釈時に求められる分析者として必須の謙虚さを与えてくれます。
注意点
この例を通し、semopyを使用したSEMの基本的な分析フローを理解できますが、実際の分析では、より複雑なモデルやデータ構造を扱うことになるため、モデルの適切な仕様設定と理論的根拠の確認が重要になります。
モデルの適合度が高いということは、そのモデルが観測データによく合致していることを示しますが、それが唯一の説明や最も正しい理論モデルであることを意味するわけではありません。実際には、異なる仮説や理論モデルが同じデータに対して高い適合度を示すことがあり、これらのモデル間でどれを選択するかの判断は容易ではありません。
この点は、特に社会科学の分野で顕著です。社会現象は多くの場合、複数の因子によって形成され、これらの因子の相互作用も考慮する必要があります。したがって、同じ現象を説明するために異なる理論が提案され、それぞれ異なる因果モデルが構築されることがあります。このため、モデルの適合度を評価する際には、以下の点を考慮するようにしましょう:
- 理論的妥当性:モデルが理論的に意味のある仮説に基づいているかどうか。
- モデルの単純さ:オッカムの剃刀の原則に従い、過度に複雑ではないモデルが好まれる場合があります。
- 代替モデルの検討:他のモデルと比較して適合度が高いかどうか、または異なる理論モデルが同じデータにどのように適合するかを評価する。
適合度の高いモデルが複数存在する場合は、適合度のような定量的基準に、理論的な説明力と解釈の容易さなどの質的判断基を加え、最も適切なモデルを選択する質的判断力が必要です。モデルの適合度は、そのモデルの有効性の一指標であると同時に、さまざまな因果モデルを探究する出発点なのだと理解しておきましょう。
結論
構造方程式モデリングは、複雑な因果関係の探究と理論的枠組みの検証に非常に有効な手法です。この手法を利用することで、潜在変数を含む複雑なモデルを構築し、より洞察に富んだ分析結果を得ることができます。
会員サービスについて見る
CIが運営する会員サービスにご登録いただくと、この記事で取り上げた内容をわかりやすく解説した動画にアクセスできるようになります。会員サービスの中身については、以下のページをご参照ください。年4回程度を目安に、新規会員受付けのための待機リストを公開しています。リストが公開されている際は、ぜひご登録ください。
















[…] (※注:論文ではアンケート調査とインタビュー、観察をもとに、構造方程式モデリング(SEM)分析という統計的分析処理を行っていました) […]
Joinery Manufacturing Inverness
構造方程式モデリング入門:因果関係を正しく理解するためのガイド