はじめに
意思決定において、統計分析は欠かせない役割を果たしています。特に、調整分析と感度分析は、データから得られる知見の信頼性を高め、意思決定の質を向上させる上で重要です。
本記事では、調整分析と感度分析の基本的な概念を説明し、両者の関係性について議論し、意思決定プロセスにおける両者の活用方法を提示します。
調整分析とは
調整分析は、交絡要因の影響を調整することで、関心のある要因と結果の因果関係を正しく推定することを目的とします。たとえば、喫煙と肺がんの関係を調べる際、年齢などの交絡要因の影響を調整することで、喫煙の影響をより正確に評価しようとします。
調整分析の代表的な手法には、層別解析や重回帰分析などがあります。層別解析では、交絡要因ごとにデータを分割し、各層内で関心のある要因と結果の関係を評価し統合します。たとえば、年齢層ごとに喫煙と肺がんの関連を調べ、年齢層の影響を調整します。重回帰分析では、複数の交絡要因を同時にモデルに含めることで、それらの影響をまとめて調整します。具体的には、肺がんの有無を目的変数、喫煙状況を説明変数、年齢などの交絡要因を共変量とした回帰モデルを構築することで、喫煙の影響を調整します。
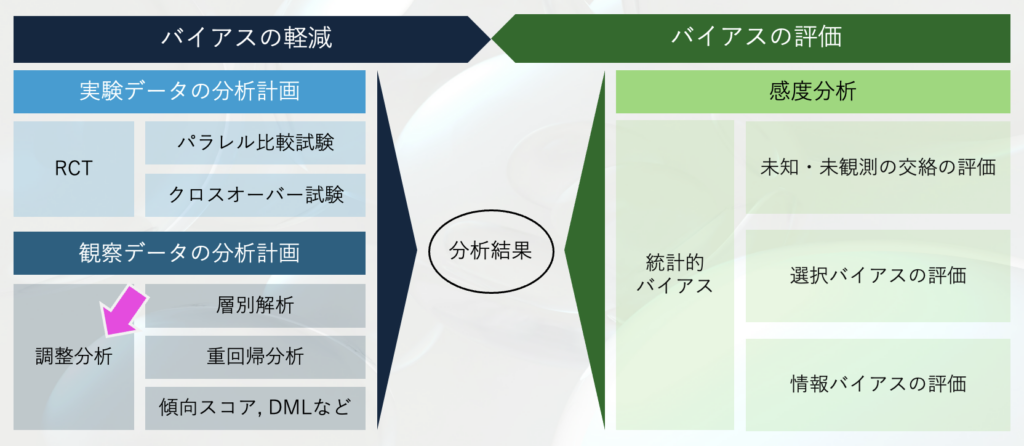
近年では、機械学習を用いたDouble Machine Learning(DML)による高次元データへの対応も可能になっています。DMLは、交絡要因と結果、および交絡要因と関心のある要因の関係を別々にモデル化し、データの異質性を考慮することで、より精度の高い因果効果の推定を目指します。このアプローチにより、高次元の交絡要因や非線形関係の柔軟な調整が可能となり、異なるサブグループ間での因果効果の変動も捉えられます。
DMLとは
DMLのモデルは、アウトカムY、処置変数T(関心のある要因)、異質性に関わる交絡要因X、その他交絡要因W、操作変数をZとすると、以下のように表現できます。
☑️ 処置変数Tのモデル
Tは、交絡要因XとW、そして操作変数Zの関数としてモデル化されます。Zは、Tに直接影響を与えるが、Yには直接影響を与えない変数であり、TとYの因果関係の推定において重要な役割を果たします。
☑️ アウトカムYのモデル
Yは、処置変数Tの予測値(たとえば、Tに対する機械学習モデルを通じて得られた予測値)、それと交絡要因XとWの関数としてモデル化されます。
この厳密な設定により、DMLはTとYの間の因果効果を、XとWの影響から調整し、より正確に個別化して推定することができます。操作変数Zの使用は、特に関心のある要因Tがランダムに割り当てられない場合(たとえば観察データにおいて)に、因果関係の識別に役立ちます(より詳しい解説は、Microsoftの因果推論ライブラリEconMLの公式ドキュメントを参照ください)。
ただ、調整分析にも限界があり、未知・未観測の交絡要因が存在する場合や、データ測定時に生じる情報バイアスに対しては対処できません。そのため、調整分析の分析結果であっても、常に控えめに解釈する必要があります。
感度分析とは
感度分析は、分析結果の頑健性の評価を目指したものです。中でも、E-valueと呼ばれる指標を用いると、どの程度の影響力をもった未知の交絡要因の存在によって、調整分析によって得られた分析結果が覆され得るかを評価できます。
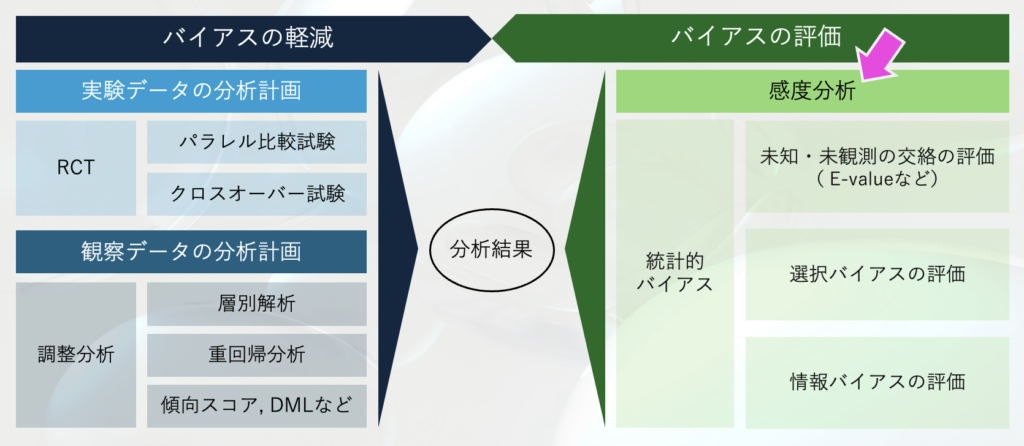
E-valueとは、関心のある要因と結果の関連性を覆すために必要な、未知・未観測の交絡要因の「最小限の関連強度」を表す指標です。この指標の解釈を先に書くと、以下のようになります。
- E-valueが高い場合、分析結果は未知の交絡要因により覆りにくい。
- E-valueが低い場合、分析結果は未知の交絡要因により覆りやすい。
たとえば、喫煙と肺がんの関係を調べた分析結果を覆すような未知の交絡要因Uが存在すると仮定すると、その要因UのE-valueは、相当に高い数値になるだろうということです。
E-valueとは
E-valueは、未知・未観測の交絡要因Uが、観察データの分析で推定された、結果Yと暴露E(関心のある要因)の間の関連性(リスク比:RR_obs)を完全に説明(覆す)ために必要な強さを表す指標です。E-valueが高ければ、RR_obsは未知の交絡要因の存在によって容易には1.0に戻らず、逆に低ければ、RR_obsは1.0に戻りやすいと解釈できます。
もう少し具体的に記述してみます。仮にE-valueがeの場合、以下の二つの条件が同時に成立する時などに、RR_obsは1.0(null-value)に戻ります。
条件❶:UYの関連性(未知要因Uが結果Yに与える影響)に関する条件
UYは、未知の交絡要因Uが結果Yのリスクをどれだけ増加させるかを表します。この強さは、たとえばリスク比で表される。この場合、関連性はUがYのリスクをどれだけ増加させるのリスクで表現され、結果のnull-value化には、未知要因Uはこれをe倍高めなければなりません。
条件❷:UEの関連性(未知要因Uが暴露Eに与える影響)に関する条件
UEは、未知の交絡要因Uが暴露Eの中でどれだけ偏っているかを表します。この偏りを示す一つの方法は「暴露群におけるUの存在割合÷非暴露群におけるUの存在割合」を計算することです。結果のnull-value化には、未知要因の分布の偏りを示すこの割合がe倍偏ってなければなりません。
また、詳細は省きますが、E-valueの計算は、未知要因Uの(観察集団における)存在割合(relevence)を仮定していないため、計算されたその値は、観察データから推定された暴露(関心のある要因)と結果間の関連性をnull-valueに戻すのに必要な「最小限の関連強度」を示します。
この特性により、E-valueの解釈は、最も保守的な解釈となります。このことから、分析者は、分析結果を覆し得る最小限の影響を持つ未知要因の存在を検討することができるのです。つまり「UY=UE=最小関連強度(e)となるような、未知要因は果たして存在するのか?」と、分析者はドメイン知識に照らして問うことができるのです。
以上から、E-valueは、分析の結果解釈の信頼性を高めるために有効な手段として認識され活用されています。これは特に、観察研究における因果推論の文脈で重要であり、未知・未観測の交絡要因の影響を考慮しながら、推定された変数間の関連性の解釈に役立ちます。
ただ、感度分析は、調整分析では扱えない未知・未観測の交絡要因の影響を評価するものであり、未知の交絡要因の存在については何ら示してはくれません。未知・未観測の交絡要因の存在を主張するには、分析者のドメイン知識とそれに基づく質的判断に依存します。
調整分析と感度分析の関係
調整分析と感度分析とでは、扱う交絡要因の種類が異なります。調整分析は観測された交絡要因を対象とするのに対し、感度分析は未知・未観測の交絡要因を対象とします。ちなみに、DMLは観測された高次元の交絡要因への対応という点で、調整分析の範疇に属すると言えます。
調整分析と感度分析は、相補的な関係です。調整分析で観測された交絡要因を調整した後、感度分析で未知・未観測の交絡要因等の影響を評価することで、結果の頑健性をより詳細に検討できます。
意思決定における調整分析と感度分析の活用
調整分析により因果効果を推定し、感度分析によりその結果の頑健性を評価することで、意思決定プロセスの改善が期待できます。観察データには限界があるため、両者を組み合わせることで、データから得られた知見の証拠能力が高まり、より確かな意思決定へと繋がります。
たとえば、一部店舗での販促キャンペーンを実施し、調整分析により販促効果を推定したとします。ここで、感度分析を加え結果の頑健性を評価することで、販促展開の大規模化に踏み切りやすくなるでしょう。調整分析で効果を推定し、感度分析でその結果の頑健性を評価することで、データに基づく意思決定が一層推進されるのです。
キャンペーン効果の感度分析イメージ
たとえば、以下のようなステップで分析を進めることが想定できます。
- 調整分析
- 処置変数:キャンペーン実施有無(1:実施, 0:非実施)
- アウトカム:購買力(売上高や購買金額など)
- 交絡要因:店舗の立地、規模、過去の売上実績など
- 調整分析により、キャンペーンの効果(因果効果)を推定
- 感度分析
- 調整分析で推定された処置変数とアウトカムの関連性について、E-valueを計算
- E-valueの値に基づいて、調整分析の結果の頑健性を評価
- 👉 E-valueが高ければ、未知の交絡要因が結果を覆すためには強い関連性が必要であり、結果は頑健であると解釈
- 👉 E-valueが低ければ、未知の交絡要因が結果を覆すために必要な関連性は比較的弱く、結果は頑健でないと解釈
- 意思決定
- 調整分析と感度分析の結果を総合的に判断
- 👉 調整分析で考慮されなかった未知の交絡要因(例:天候、競合他社の動向、地域のイベントなど)に関する過去の分析結果を参照し、E-valueの高さが十分かを論じる。
- 👉 この過去分析結果の参照時に、確証バイアスなどの認知バイアス、および選択的報告に陥らないように十分に注意する。
- 推定されたキャンペーン効果の大きさと、その結果の頑健性を考慮しながら、キャンペーンの継続や拡大についての意思決定を行う
- 調整分析と感度分析の結果を総合的に判断
このように、処置変数がバイナリ変数、アウトカムが連続変数の場合でも、調整分析と感度分析を組み合わせることで、キャンペーンの効果についてより確かな意思決定を行うことができます。
ただ、調整分析と感度分析の両方を行っても、分析結果の質は、依然として分析仮定(モデルの妥当性)の影響を受けています。そのため、特に観察データに基づく意思決定は、常に謙虚である必要があります。
まとめ
調整分析と感度分析は、分析において重要な役割を果たします。両者を適切に活用することで、意思決定の質を高めることができ、今後もこれらの手法の発展が期待されています。特に、DMLによる異質性や高次元データへの対応や感度分析への理解を深めることは有益でしょう。
また、意思決定者は、調整分析と感度分析の基本的な概念を理解し、両者の活用を組織的に推進することで、データに基づく確かな意思決定の恩恵を手に入れられます。
会員サービスについて見る
CIが運営する会員サービスにご登録いただくと、この記事で取り上げた内容をわかりやすく解説した動画にアクセスできるようになります。会員サービスの中身については、以下のページをご参照ください。年4回程度を目安に、新規会員受付けのための待機リストを公開しています。リストが公開されている際は、ぜひご登録ください。















Comment