はじめに
ビジネス施策の効果検証に際し、大変参考になる『Pythonで学ぶ効果検証入門』(オーム社)で statsmodels.formula.api が使われていたので、このapiを使う上での注意点や書籍では触れられていなかった一般化線形モデル(GLM)について紹介します。
なぜOLSで統一したのだろうか?
書籍の2章を改めて見ると、GLMの話題は意図的に省かれているように感じました。ロジスティック回帰、ポアソン回帰などを紹介するメリットと実務的なリターンを天秤にかけたのではないかと。ただ、これは一読者の勝手な想像のため、著者のサポートページのデータを使って、天秤にかけたであろう内容を確認してみることにしました。
目的変数がバイナリのケース
サポートページのデータによる比較
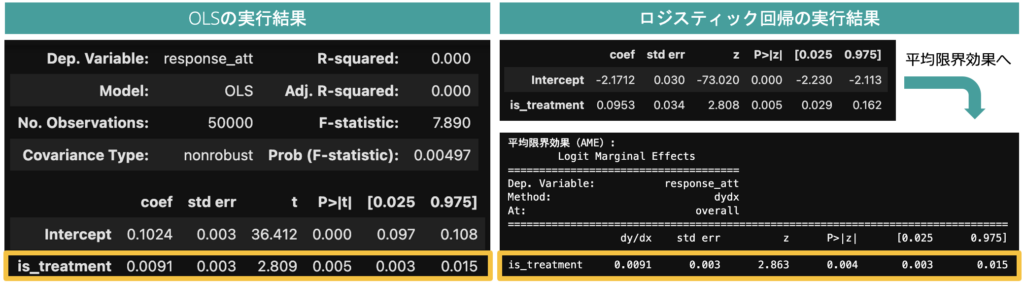
著者サポートページにあるデータ(lenta_dataset)を使って推定結果を比較すると、このデータ(処置群:37691件、対照群:12309件)の場合、OLSとロジスティック回帰の間で処置効果の推定結果にほとんど差が生じないことがわかります。
ロジスティック回帰はモデル表現に非線形変換を含み、summary関数で出力される回帰係数の直感的な解釈が難しいため、OLSのように解釈をするには「平均限界効果」の理解とその計算が必要になります(平均限界効果は「各行の説明変数を1単位変化させた際の目的変数の変化量(限界効果)」を平均したもので、get_margeff関数で計算できます)。
人工データによるシミュレーション
OLSとロジスティック回帰の推定結果の差異を把握するため、下記条件の人工データを使って確認してみます(シミュレーション条件は最後にご案内している「特典コード」内で変更可能です)。
・対照群のフラグ割合:処置群よりも2.5%低い
・目的変数のフラグは scipy.stats.bernoulli を使って生成
シミュレーション結果①
処置群を375件、対照群を125件とした際の推定結果を比較すると、回帰係数の標準誤差の違いのために、信頼区間やp値に差異が生じることを確認できます(注意:ランダムシードをある値に固定した単一の結果比較です)。
図2:人工データに基づくOLSとロジスティック回帰の推定結果の比較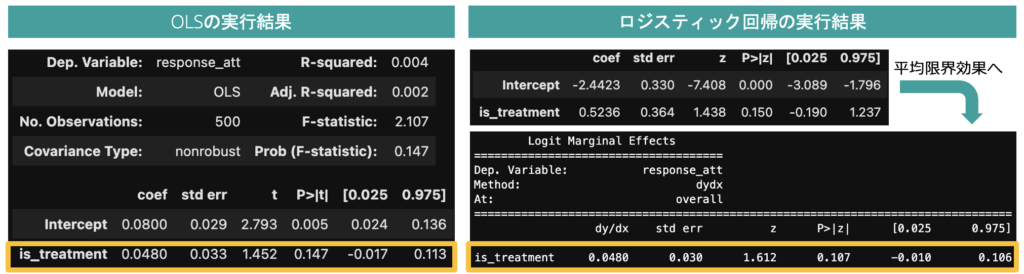
シミュレーション結果②
ランダムシードを固定せず、データの生成と推定を1000回繰り返した際のp値と回帰係数の分布は以下の通りで、p値の分布に違いが見られます。ロジスティック回帰の方が、本来ある差を「有意ある差」として検出してくれる傾向にあることがわかります。
図3:人工データに対する推定を1000回行った際の推定結果比較(size=500)
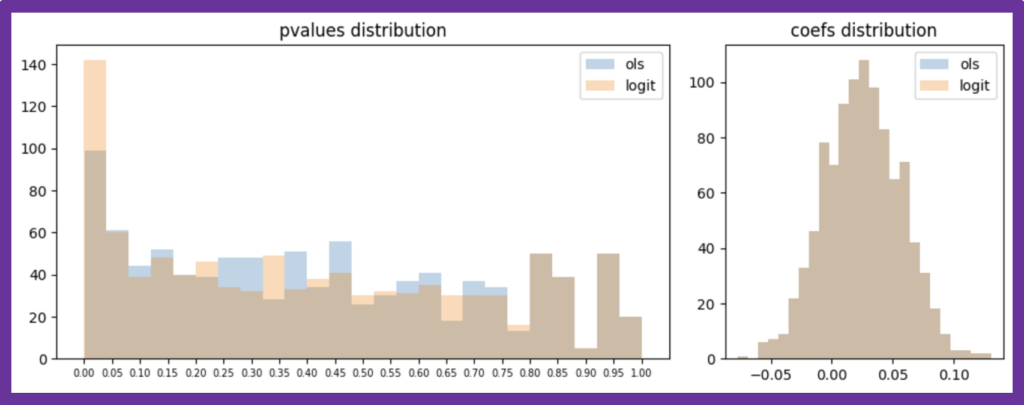
次に、人工データのサンプルサイズを500から5000へと増やしてみます。偶然誤差が減少するため、点推定値だけでなく、p値の分布の差もほとんど見られなくなりました。特に、数万規模が珍しくないデジタル施策のA/Bテストでは、OLSでサッと計算しても実務的な害はほとんど生じないことが予想できるでしょう。
図4:人工データに対する推定を1000回行った際の推定結果比較(size=5000)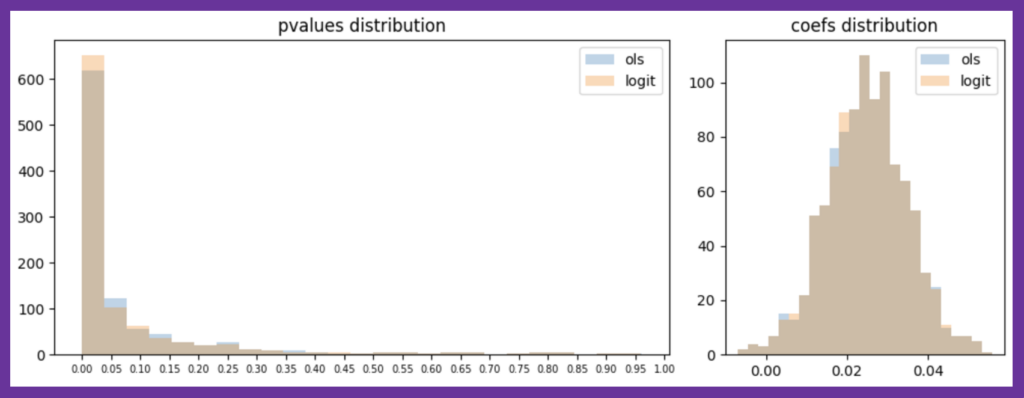
目的変数がカウントデータのケース
最後に、カウントデータの目的変数に対応したポアソン回帰の推定結果をOLSと比較することにします。データは、以下の人工データを使います。
・対照群:15000人、平均値1.8のポアソン分布に従うカウントデータを生成
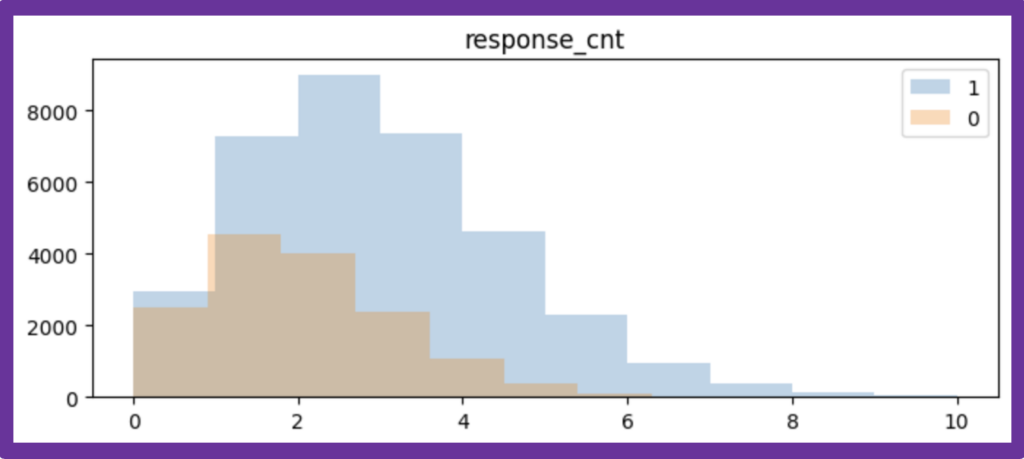
以下は、あるランダムシード時の人工データに対する推定結果の一例ですが、双方のモデルの推定結果に差異はほとんど見られませんでした。
図6:人工データに基づくOLSとポアソン回帰の推定結果の比較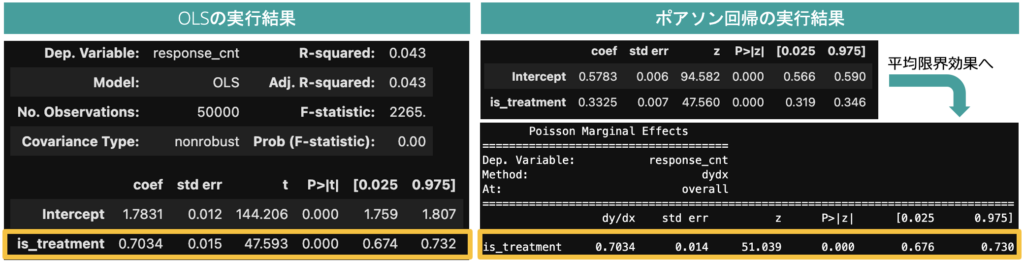
サンプルサイズを50000人から500人(処置群:350人、対照群:150人)へ落とし、対照軍の平均値を2.3とした上で、データの生成と推定を1000回繰り返した際の結果は、以下の通りです。差の検出を難しくしても、双方の推定結果にほとんど差異は見られません。
図7:人工データに対する推定を1000回行った際の推定結果比較(sample_size=500)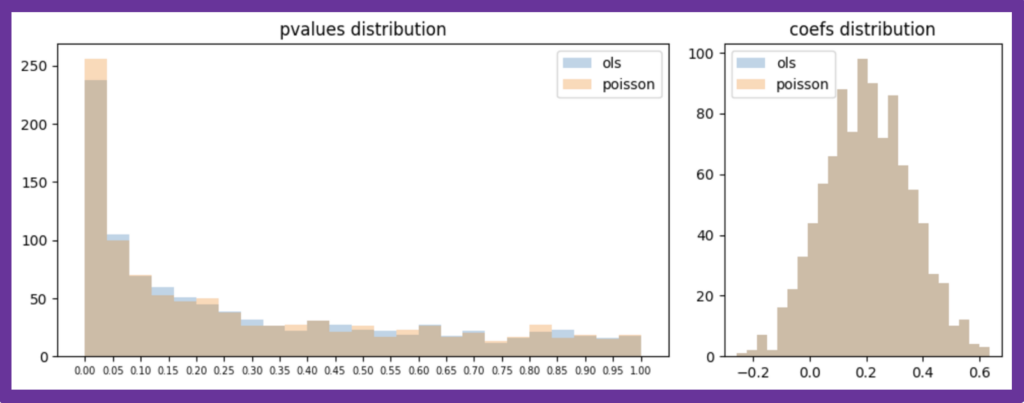
一般化線形モデルに習熟した人が、カウントデータに対しあえてOLSを利用する動機はないでしょうが、実際の分析の文脈において、そのモデル選択がどの程度の精度差を生み出しているのかの確認をしてみると、想像よりも意外と小さい効果しかないかもしれません。
注意:平均限界効果の計算に際して
平均限界効果を得るためのget_margeff関数の引数dummyの初期値はFalseですが、これはバイナリの説明変数を連続変数として扱うため、このままだと変数is_treatmentの平均限界効果の推定値を狂わせます。
以下が、dummy=Flase(初期値)の場合と、Trueの場合の推定結果の違いです。
図8:get_margeff関数の引数dummyの初期値(False)の影響

初期値をそのまま使うと、データ生成過程に整合したモデルを選択しているにも関わらず、点推定値に(OLSにも見られない)バイアスが生じることになります。
オープンソースライブラリの利用に見られる、この種の「初期値バイアス」には十分に注意しましょう。
まとめ
今回は、『Pythonで学ぶ効果検証入門』(オーム社)で紹介されているOLSベースの回帰分析と一般化線形モデルの推定結果の比較を行いました。データ生成に整合的なモデルを選択することで、効果推定量の標準誤差(信頼区間やp値)の推定結果に差が生じることがわかりました。
ただ、特にデジタル領域における大規模A/Bテストの文脈では、両者の差は無視できるほど小さくなることも示唆されました。データ分析業務において重要なのは、実際のデータ分析の文脈において求められる分析精度を認識した上で、実効性の高い合理的な手法を選択することだと言えるでしょう。
無料特典のご案内
無料特典登録をしてもらうと、このブログ記事に用いた原稿、Pythonサンプルコード、データの3点を無料でダウンロードいただけます。















Comment