はじめに
scikit-learn の分類器の多くは predict_proba で確率を出しますが、その”確率”が実際の確率と一致している保証はありません。例えば「90%の確率で陽性」と出力されても、実際には「70%」しか正解していない…ということもしばしば起こります。
こんな時、CalibratedClassifierCV を使うと、こうした確率のズレを補正し確率の信頼性を向上させることができます。特にアンサンブル学習の予測確率は極端な値になることがあるため、この校正の効果が得られる可能性があります。
ハイパーパラメータ
以下、CalibratedClassifierCV のハイパーパラメータとその内容です。確率校正器は、与えられた estimator の decision_score(ない場合には predict_proba )の値が評価データに適合するように調整されます。
キャリブレーション方法(method)は二種類で、比較的単純な調整(線形的な調整)で済む場合にはシグモイド関数のパラメータ調整を、データが十分にありより複雑な変換が必要そうな場合には、isotonic 設定を検討します。
- sigmoid:
- ロジスティック回帰で校正(比較的単純な変換)
- サンプル数が少ないとき、または高速に済ませたいとき
- isotonic:
- より柔軟な非線形変換
- サンプル数が十分なとき
他のパラメータである交差検証(cv)やアンサンブル(ensemble)の設定については、節を分けて詳しく解説します。
キャリブレーションの実行
CalibratedClassifierCV では、単に分類器を構築するのではなく、predict_proba の出力が検証データと整合するように調整されます。以下、CalibratedClassifierCV を使った校正の流れです。
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.calibration import CalibratedClassifierCV
# 訓練用と検証用にデータを分割
X, y = load_breast_cancer(return_X_y=True, as_frame=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# 未校正の分類器を定義
clf = RandomForestClassifier(random_state=0)
# 校正付き分類器を定義
calibrated_clf = CalibratedClassifierCV(
estimator=clf,
method='sigmoid', # または 'isotonic'
cv=5, # 5-fold CV で校正
ensemble="auto" # 凍結(Frozen)された estimator の場合、自動で False 扱いになる
)
# 学習
calibrated_clf.fit(X_train, y_train)
# 校正された確率を使って予測
calibrated_probs = calibrated_clf.predict_proba(X_test)確率校正の比較実験
以下4つのパターンで確率校正効果の比較実験を行うため、❶校正効果の測り方、❷分類器の凍結、❸校正時のアンサンブルについて解説します。
校正の効果をどう測るか?
単なる分類精度(accuracyやAUC)は「予測の正確さ」を測るものであり、確率自体の信頼性を評価するものではありません。そこで役立つのが、Brierスコアのような確率校正指標です。
この指標は「予測確率と実際の結果の差」を数値化し、校正によってモデルの確率出力がどれだけ現実に近づいたかを定量的に示します。この値が小さいほど、予測確率が現実に近いと評価できます。
分類器の凍結とは何か?
CalibratedClassifierCV では通常、内部で estimator.fit() を呼び出し分類器を学習します。しかし、すでに十分に学習されたモデルがある場合、モデルは再学習させずに「校正だけ」行わせたい場合が少なくありません。
こんな時に役立つのがモデルの訓練を凍結してくれる FrozenEstimator です。これにより CalibratedClassifierCV 内部の分類器は固定され、予測確率と実際の結果の対応関係に基づく校正だけ行わせられます。
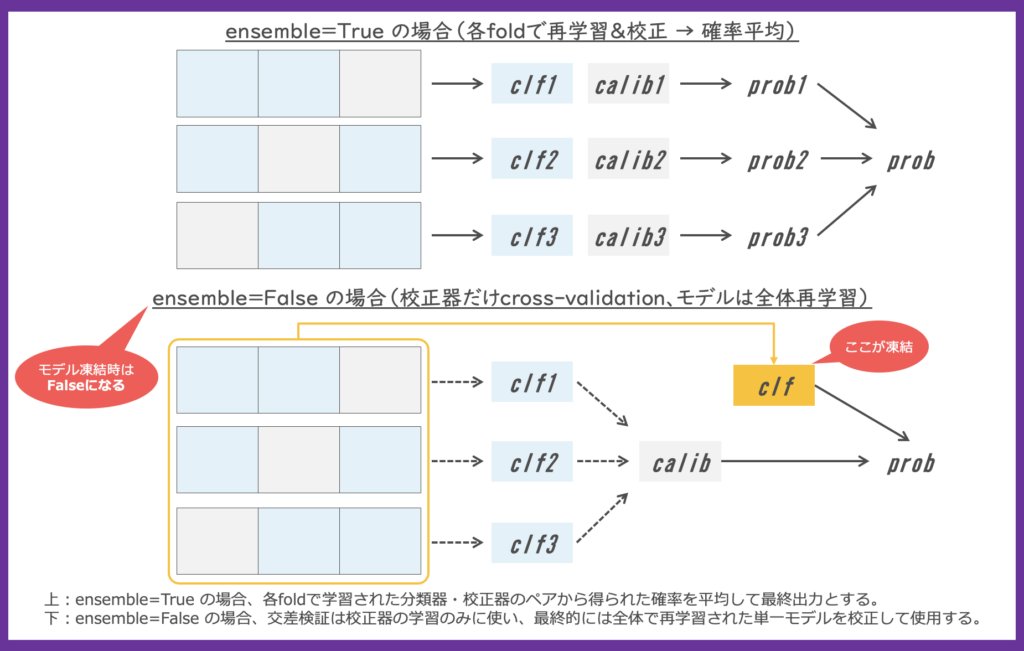
アンサンブルとは何か?
CalibratedClassifierCV で ensemble=True とすると、交差検証の fold ごとにモデルの訓練と校正が行われ、それら予測確率の平均値を返す統合的なプロセスが採用されます。ensemble=False とすると、交差検証で(仮の分類器と)最良の校正ロジックが決定され、分類器は全てのデータから一つ構築されます。
ensemble のデフォルトは “auto” ですが、先のモデル凍結が指定された場合には ensemble=False となり、分類器は指定の学習済みモデルが使われます。
校正効果の比較
パラメータ理解ができたところで、以下の4つのモデルを比較する実行コードを確認します。
実行コード
# ライブラリの読み込み
from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.frozen import FrozenEstimator
from sklearn.calibration import CalibratedClassifierCV
from sklearn.metrics import brier_score_loss
from sklearn.model_selection import train_test_split
# データ作成
X, y = load_breast_cancer(return_X_y=True, as_frame=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# 校正なしの分類器
clf_org = RandomForestClassifier(random_state=0)
clf_org.fit(X_train, y_train)
probs_uncalibrated = clf_org.predict_proba(X_test)[:,1]
# 校正あり分類器再学習 (ensemble='auto'=True)
clf = RandomForestClassifier(random_state=0)
calibrated_clf_ens = CalibratedClassifierCV(estimator=clf, method='sigmoid', cv=5)
calibrated_clf_ens.fit(X_train, y_train)
probs_calibrated_ens = calibrated_clf_ens.predict_proba(X_test)[:,1]
# 校正あり分類器再学習 (ensemble=False)
clf = RandomForestClassifier(random_state=0)
calibrated_clf_not_ens = CalibratedClassifierCV(estimator=clf, method='sigmoid', cv=5, ensemble=False)
calibrated_clf_not_ens.fit(X_train, y_train)
probs_calibrated_not_ens = calibrated_clf_not_ens.predict_proba(X_test)[:,1]
# 校正あり分類器凍結 (ensemble='auto'=False)
clf_org_frozen = FrozenEstimator(clf_org)
calibrated_frozen_clf = CalibratedClassifierCV(clf_org_frozen, method='sigmoid', cv=5)
calibrated_frozen_clf.fit(X_train, y_train)
probs_calibrated_frozen = calibrated_frozen_clf.predict_proba(X_test)[:,1]
# Brierスコアで比較
score_uncalibrated = brier_score_loss(y_test, probs_uncalibrated)
score_calibrated_ens = brier_score_loss(y_test, probs_calibrated_ens)
score_calibrated_not_ens = brier_score_loss(y_test, probs_calibrated_not_ens)
score_calibrated_frozen = brier_score_loss(y_test, probs_calibrated_frozen)
print(f"Brierスコア(校正なし): {score_uncalibrated:.4f}")
print(f"Brierスコア(校正あり再学習/ensemble): {score_calibrated_ens:.4f}")
print(f"Brierスコア(校正あり再学習/not ensemble): {score_calibrated_not_ens:.4f}")
print(f"Brierスコア(校正あり凍結版): {score_calibrated_frozen:.4f}")結果の可視化
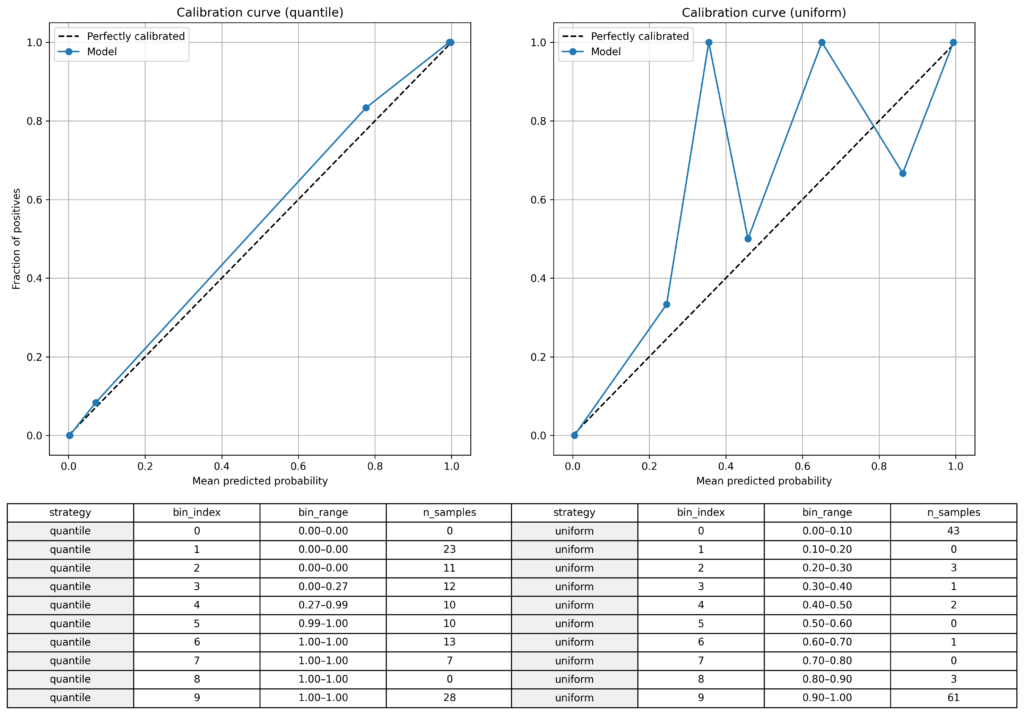
Brierスコアだけでは、効果を体感することが難しいでしょうから、結果を可視化して伝えることが大切です。ここで役立つのが calibration_curve を使った可視化です。以下の異なるビニング戦略を併記しておくとよいでしょう。
- strategy=’quantile’ : 区間別サンプル数が等しくなるように区間定義
- strategy=’uniform’ : 区間幅を等分割
描画に必要なライブラリを追加で読み込みます。
# ライブラリの読み込み
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.calibration import calibration_curve描画したい予測確率の配列情報を与えておきます。
# 描画対象の予測確率の配列
probs = probs_uncalibratedビニング戦略別にキャリブレーションカーブを描きます。
# ビン境界を取得する関数
def get_bins(y_prob, n_bins=10, strategy='uniform'):
if strategy == 'uniform':
bins = np.linspace(0.0, 1.0, n_bins + 1)
elif strategy == 'quantile':
bins = np.quantile(y_prob, q=np.linspace(0.0, 1.0, n_bins + 1))
else:
raise ValueError("strategy must be 'uniform' or 'quantile'")
return bins
# ビン情報の取得
strategies = ['uniform', 'quantile']
bin_data = []
for strat in strategies:
bins = get_bins(probs, n_bins=10, strategy=strat)
bin_counts = np.histogram(probs, bins=bins)[0]
for i in range(len(bin_counts)):
bin_data.append({
'strategy': strat,
'bin_index': i,
'bin_range': f"{bins[i]:.2f}–{bins[i+1]:.2f}",
'n_samples': bin_counts[i]
})
df_bins = pd.DataFrame(bin_data)
df_q = df_bins[df_bins['strategy'] == 'quantile'].reset_index(drop=True)
df_u = df_bins[df_bins['strategy'] == 'uniform'].reset_index(drop=True)
# calibration curve 出力
fraction_quantile, mean_quantile = calibration_curve(
y_true=y_test, y_prob=probs, n_bins=10, strategy='quantile'
)
fraction_uniform, mean_uniform = calibration_curve(
y_true=y_test, y_prob=probs, n_bins=10, strategy='uniform'
)
# プロット作成
fig, axes = plt.subplots(2, 2, figsize=(14, 10), gridspec_kw={'height_ratios': [2, 1]})
# 上段:calibration curve plots
ax1, ax2 = axes[0]
ax1.plot([0, 1], [0, 1], 'k--', label='Perfectly calibrated')
ax1.plot(mean_quantile, fraction_quantile, marker='o', label='Model')
ax1.set_title('Calibration curve (quantile)')
ax1.set_xlabel('Mean predicted probability')
ax1.set_ylabel('Fraction of positives')
ax1.legend()
ax1.grid(True)
ax2.plot([0, 1], [0, 1], 'k--', label='Perfectly calibrated')
ax2.plot(mean_uniform, fraction_uniform, marker='o', label='Model')
ax2.set_title('Calibration curve (uniform)')
ax2.set_xlabel('Mean predicted probability')
ax2.legend()
ax2.grid(True)
# 下段:テーブル
ax_table_q, ax_table_u = axes[1]
ax_table_q.axis('off')
ax_table_u.axis('off')
# matplotlib テーブル(quantile)
table_q = ax_table_q.table(cellText=df_q.values,
colLabels=df_q.columns,
cellLoc='center',
loc='center')
table_q.auto_set_font_size(False)
table_q.set_fontsize(10)
table_q.scale(1.2, 1.2)
# matplotlib テーブル(uniform)
table_u = ax_table_u.table(cellText=df_u.values,
colLabels=df_u.columns,
cellLoc='center',
loc='center')
table_u.auto_set_font_size(False)
table_u.set_fontsize(10)
table_u.scale(1.2, 1.2)
# strategy列(列インデックス0)の背景色をグレーに
for row_idx in range(len(df_q)):
table_q[(row_idx + 1, 0)].set_facecolor('#f0f0f0') # +1 はヘッダー行の分
for row_idx in range(len(df_u)):
table_u[(row_idx + 1, 0)].set_facecolor('#f0f0f0')
plt.tight_layout()
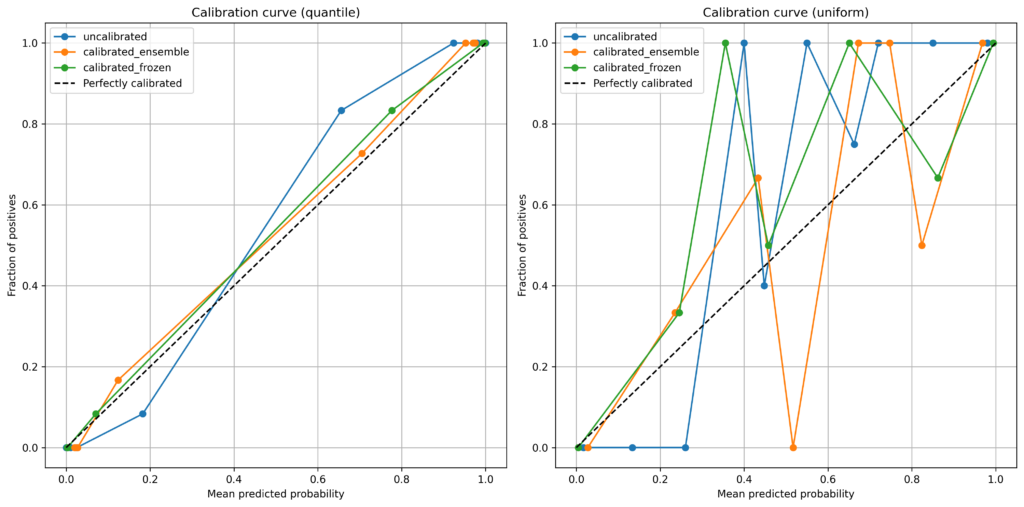
plt.show()最後に、複数のキャリブレーション結果を比較するための可視化コードです。ここまでの内容を理解しておけば、この種の可視化コードはいつでもLLMに指示を出して作ることができるのであまり気にする必要はないでしょう。
# 各モデルの予測確率を取得
probs_dict = {}
probs_dict['uncalibrated'] = probs_uncalibrated
probs_dict['calibrated_ensemble'] = probs_calibrated_ens
probs_dict['calibrated_frozen'] = probs_calibrated_frozen
colors = ['C0', 'C1', 'C2']実行は以下のコードで行えます。
# プロット作成(左右に並べて表示)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 7))
for idx, (model_name, probs) in enumerate(probs_dict.items()):
color = colors[idx]
# calibration curve: quantile
fq, mq = calibration_curve(y_test, probs, n_bins=10, strategy='quantile')
ax1.plot(mq, fq, marker='o', label=model_name, color=color)
# calibration curve: uniform
fu, mu = calibration_curve(y_test, probs, n_bins=10, strategy='uniform')
ax2.plot(mu, fu, marker='o', label=model_name, color=color)
# 共通設定
for ax, title in zip([ax1, ax2], ['Calibration curve (quantile)', 'Calibration curve (uniform)']):
ax.plot([0, 1], [0, 1], 'k--', label='Perfectly calibrated')
ax.set_title(title)
ax.set_xlabel('Mean predicted probability')
ax.set_ylabel('Fraction of positives')
ax.legend()
ax.grid(True)
plt.tight_layout()
plt.show()以上です!


















Comment