概要

コンフォーマル予測（conformal prediction）は、機械学習モデルによる予測の不確実性を定量化するための手法で、回帰タスクでは予測区間を、分類タスクでは予測集合を提供します。

従来の信頼区間とは異なり、コンフォーマル予測では、例えば信頼度を95%と設定した場合、新しい観測データの95%以上が予測区間（または集合）に含まれることが保証れます（注釈：この保証は「交換可能性」などの一定の条件下で満たされます）。

この頻度論的な保証の明確さから、研究や実務応用が進み、近年急速に注目を集めています（図1）。そこで本記事では、このコンフォーマル予測の特徴について、Pythonコードとその実行結果を介して体験的に理解できるよう紹介します。

図1：「コンフォーマル予測」のGoogle Trendの推移
Source：Google Trend（2024年10月24日に取得）

予測区間（回帰タスク）

従来の信頼区間（confidence interval）の説明は、統計学に慣れた人には自然に思えるかもしれませんが、そうでない人には理解しにくいものです。

この信頼区間の解釈は、「推定を無限に繰り返した場合、そのうち95%の信頼区間が観測値を含む」というものです。しかし、ある1つの信頼区間が正解を含む確率は0か1であり、この点を直感的に理解させにくいため、説明が難しいと感じる分析者も少なくありません。

一方、コンフォーマル予測の予測区間（prediction interval）は、より直感的に説明できます。例えば、「将来の複数の観測において、その観測値の95%以上が予測区間に含まれる」といった説明が可能で、非専門家にも理解しやすいのが特徴です。

確かめたいこと

この予測区間の特徴を、シミュレーションによって確認してみましょう。具体的には、90%の信頼度で計算された予測区間に、検証用の新しい観測値（正解データ）の90%以上が含まれることを確認します。

データの生成

Rの機械学習のためのライブラリtidymodelの公式ドキュメントを参考に、これをPythonコードに置き換え、訓練用の人工データを1000件、生成しておきます（注釈：コンフォーマル予測に必要な較正データ、および検証データは後ほど生成します）。

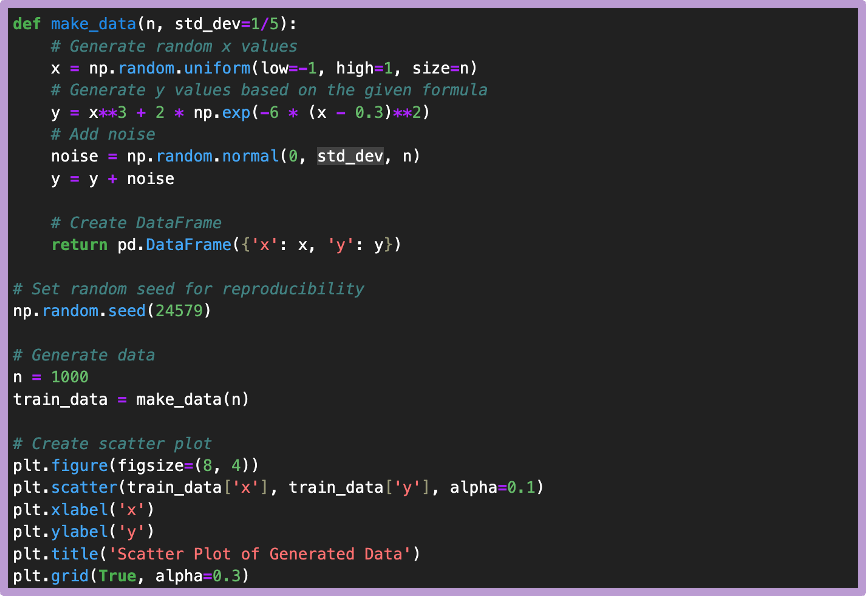
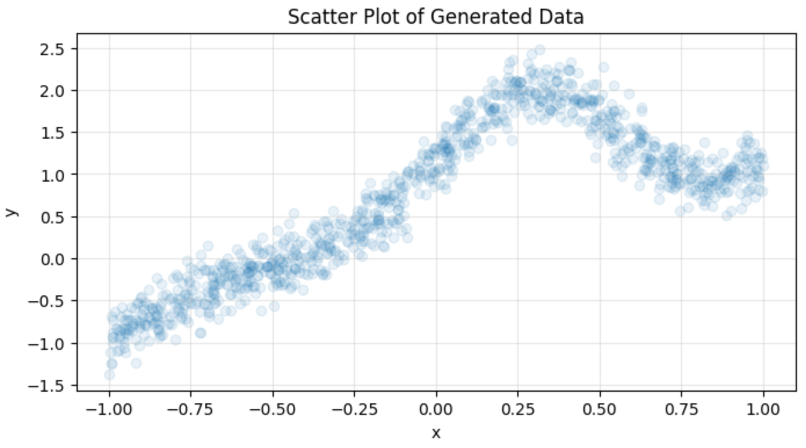
説明変数xと目的変数yの関係性は、図2の通り非線形的で、ノイズは平均0、標準偏差0.2の正規分布によって（各データポイント独立に）生成されています。

図2：人工的に生成された訓練データ

基底モデルの学習

データ生成過程で非線形な関係を導入したため、それを適切に学習できるモデルとして、カーネルリッジ回帰を採用します。参照元の記事のように、多層パーセプトロンを使っても良いですし、サポートベクターマシンや非線形項を特徴量に仕込んだ単純なリッジ回帰などでも構いません。

ただ、実務上の扱いやすさ（訓練時間の合理化）や特徴量エンジニアリングの限界（非線形項を意図して組み込む難しさ）を踏まえ、カーネルリッジ回帰を採用します（注釈：訓練処理時間に関する情報はscikit-learnの公式ドキュメントを参照）。

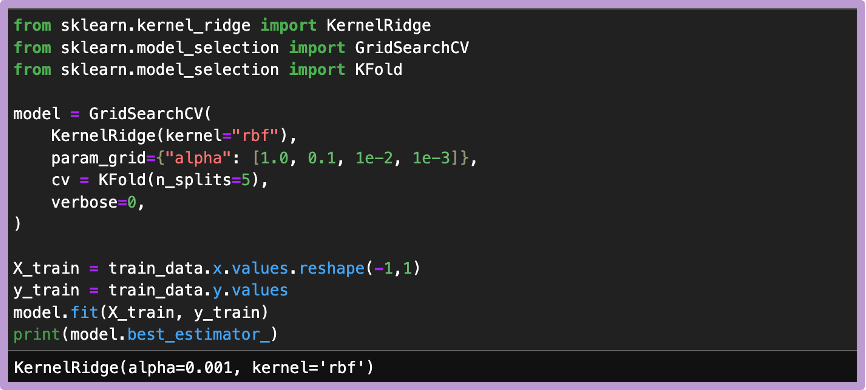
カーネルリッジ回帰の持つ初期のハイパーパラメータでは、うまく非線形関係を学習できなかったので、カーネルは固定した上で、正則化の強さαを調整しています。

また、訓練データはランダムに生成されたものなので、交差検証時にshuffleする必要はないと判断し、KFlodクラスの持つパラメータshuffleは初期値Falseのままとしました。

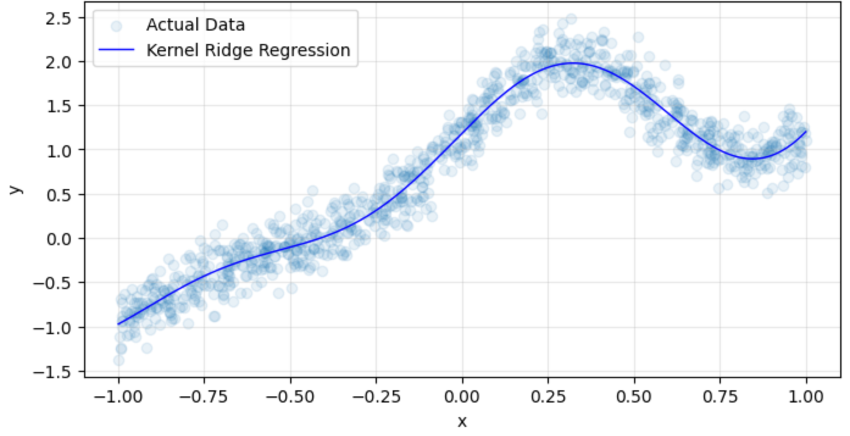
学習された関数（xとyの関係性を表す）の形状を確認するため、訓練データの上に、学習済みモデルの予測値曲線をプロットします。すると図３の通り、ノイズ影響を回避しつつ非線形関係の学習に成功している様子が伺えます。

図3：訓練データ（Actual Data）と学習済みモデルの予測値の関係

較正データ

機械学習モデリングのハイパーパラメータ調整に評価データ（validation）が用いられるように、有意水準α（信頼度1-α）の下で、コンフォーマル予測区間を計算するには、較正データ（calibration data）が用いられます。

そこで、先に作成したmake_data関数を再利用して、訓練データと同一のデータ生成過程に従う較正データと（後の検証のための）検証データを1000件ずつ生成しておきます。

このように較正データと検証データを生成しておくと、新しい観測値の(1-α)%以上が予測区間に含まれることが保証されます。この保証は「カバレッジ保証」と呼ばれ、較正データと検証データ間のデータの交換可能性（exchageable）を前提に成り立ちます（注釈：カバレッジ保証の基本定理については、分類タスクの項目で別途紹介します）。

交換可能性とは、ポーカーの手札について考えると理解しやすいです。例えば、今手元に5枚のカードがあるとして、これらが手元に同時にある確率は、それらが「手元に来た順番とは無関係」だと理解できるでしょう。このように、データの出現順序を入れ替えても、データ全体が得られる確率が変わらない性質を「交換可能性」と呼びます。

先の較正データと検証データ間の任意の点を交換しても、それらのデータ全体が得られる確率は変化しないため、交換可能性が成立します。よって、これらのデータを用いたコンフォーマル予測区間には、カバレッジ保証を満たす期待を持つことができるのです。

コンフォーマル回帰器の学習

モデルの「構築」「較正」「検証」のためのデータが揃ったので、コンフォーマル回帰器の学習を進めます。ここでは、スウェーデンのボロース大学のヘンリク・ボストルム教授によって開発されたコンフォーマル予測用のPythonライブラリcrepesを利用します。

コンフォーマル回帰器は、scikit-learnをはじめとする既存の回帰器を包含するラッパーとして実装されています。訓練データへのfitメソッドの段階で、慣れ親しんだ点推定のための回帰器が（グリッドサーチで宣言された通りに）訓練され、同時に較正のための下準備が整います。

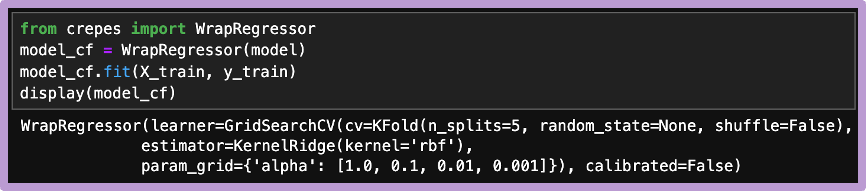
次に、予測測区間の推定のためにcalibrateメソッドを較正データに対し実行します。これで、新しいデータポイントに対する予測区間の推定ができるようになります。

ここで、有意水準α=0.1（信頼度90%）とすると、1000件の検証データ中、929件のデータが、期待通り予測区間に含まれていることを確認できます。

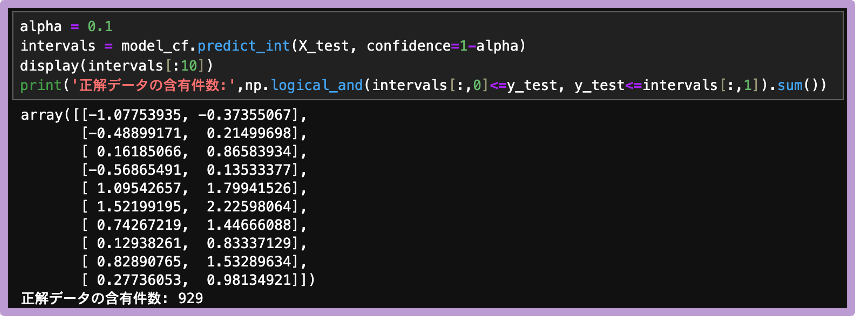
ちなみに、evaluateメソッドを使うと、予測値が予測区間に含まれない割合（エラー率）の他に、予測区間幅の平均値や中央値などを確認できます。

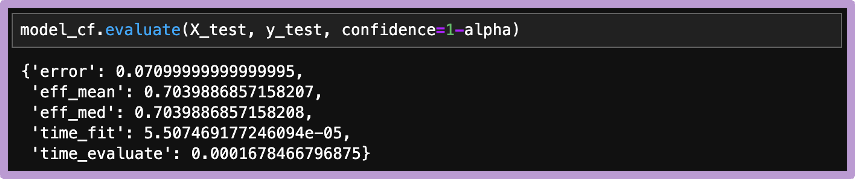
今回のエラー率は 1-(929/1000)≒0.071 で、先に設定した有意水準（α=0.1）以下に収まっています。今回のコンフォーマル予測区間の結果は、以下の図4の通りです。

図4：検証データと学習済みモデルの予測値と予測区間

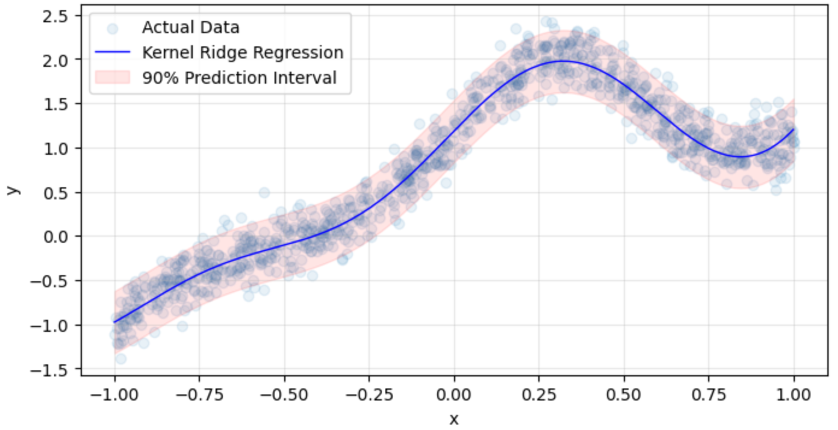
最後に、信頼度を変化させた際の、コンフォーマル予測区間に含まれる検証データの件数を確かめます。すると、予測区間のカバレッジ率は、期待通りの水準へと変化していくことがわかります。

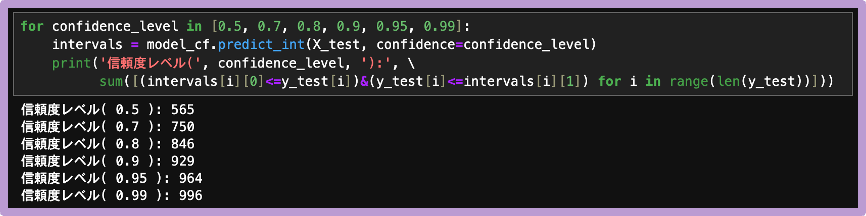
予測集合（分類タスク）

分類タスクのコンフォーマル予測では、点推定（最もらしい一つの該当クラスの予測）に留まらず、信頼度が考慮された、カバレッジ保証のある予測集合（prediction set）の推定を可能にします。

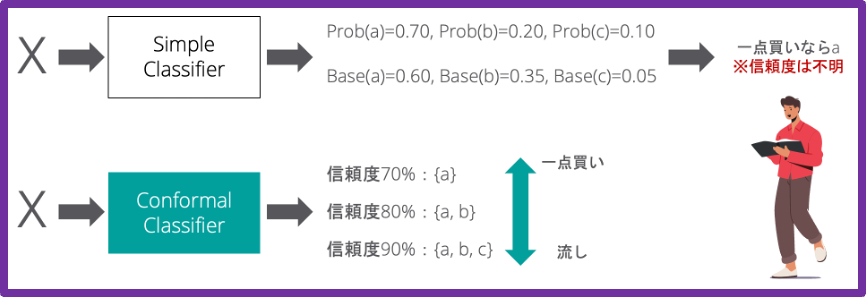
これにより、例えば、ある従業員が退職しそうな一番目、二番目、三番目の理由といった原始的な理解を超え、信頼度70%なら退職理由は{理由 a(給与)}、80%なら{ a(給与), b(上司)}、90%なら{ a(給与), b(上司), c(仕事内容)}のように、「正解理由が含まれる割合が、信頼度以上となることが保証された予測集合」の推定が可能になります。

図5：点推定から信頼度ベースの予測集合へ

予測集合がもたらす実務上の利点は想像以上に大きなものです。例えば、（退職リスクが高いと予想された）部下との初期の対話では、できるだけ高い信頼度の予測集合に基づき（退職動機を決めつけない）丁寧な対応を心掛け、対話の後期では、低い信頼度の理由に対する思い切った改善案を提示し交渉に備えるといったことが可能になります。

このような信頼度に基づくコミュニケーションは、従来の分類器の出力だけでは難しいものでした。信頼度という基準のない従来出力では、例えば予測水準は高いが、それがベースレートより低いような場合（クラスb）、そのクラスをどの程度重視して扱うかは悩ましい問題でした。

カバレッジ保証の基本定理

点推定を予測集合へと拡張する際に、コンフォーマル予測の最も基礎に位置づけられる定理があります。この定理のお陰で、私たちは「新しい観測データを任意の割合以上で含む予測集合」の作り方を理解することができます。

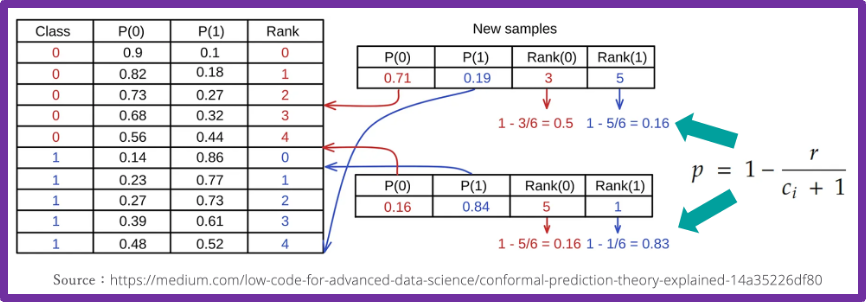
図6：予測集合の作り方とカバレッジ保証の定理

まず、左上の関数sは不適合（non-conformity）関数で、「この値が大きいほど、そのデータポイントが当該クラスに属しにくい」と解釈できるように定義します。この最もシンプルな定義は、ソフトマックス関数などで得られる各クラスの予測値p(y|x）を1から減じるというものです。

次に、p値（統計学で知られたp値とは別物）を、左側黄色括弧内の通りに求めます。このp値は「較正データ内に、新しいデータよりも不適合なものが何件あるかを数え上げ、較正データの件数(n）を使って基準化された値」で、この値が大きいほど予測集合に含まれやすくなります。

最後に、p値が「有意水準α以上の全てのクラスラベル」で予測集合を構成すると、新しい観測データの(1-α)%以上で、その正解ラベルが予測集合に含まれることが保証されます。この数学的な保証を土台に、コンフォーマル予測のライブラリは実装されています。

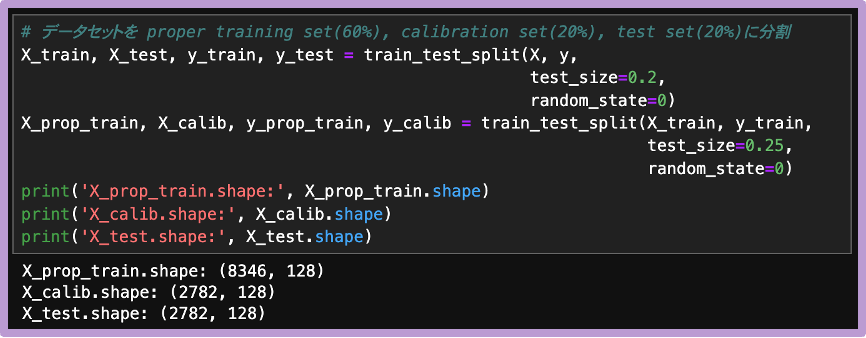
データロールの設定

p値に基づく予測集合の構成の流れを、crepesのチュートリアルページに従い確認します。データはscikit-learnのfetch_opneml関数を使って読み込みます（注釈：OpenMLは機械学習の実験やアルゴリズム比較のためのオープンなプラットフォームです）。

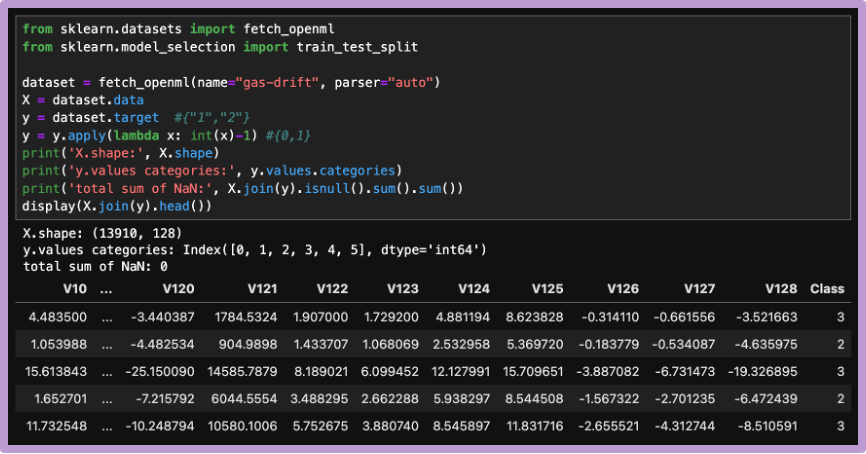
同じデータ生成過程から得られたであろうデータを、ランダムに分割し得られた較正データと検証データの間では、交換可能性が成立すると考えられるため、カバレッジ保証が成り立つと期待し、この後の確認作業を進めます。

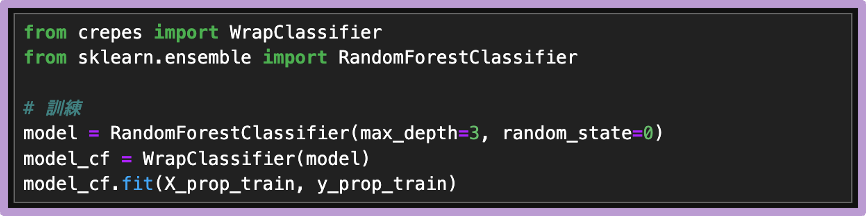
基底モデルの学習と較正準備

基底モデルにランダムフォレストを設定した上で、crepesのコンフォーマル分類器を学習させます。この段階で、基底モデルの学習と較正作業の準備が整います。

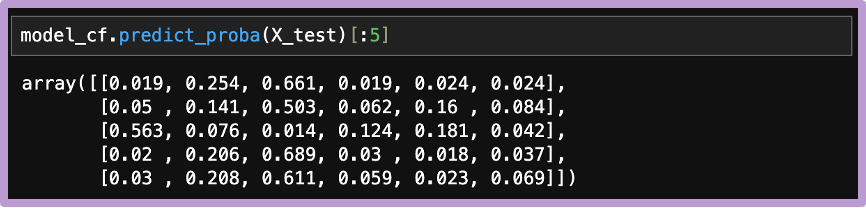
基底モデルの学習を終えているので、predict_probaメソッドを使って、クラスごとの予測値を確認することができます。

続けて、較正（予測集合を構成するために必要なp値計算のための準備）は、calibrateメソッドを実行すれば終了です。

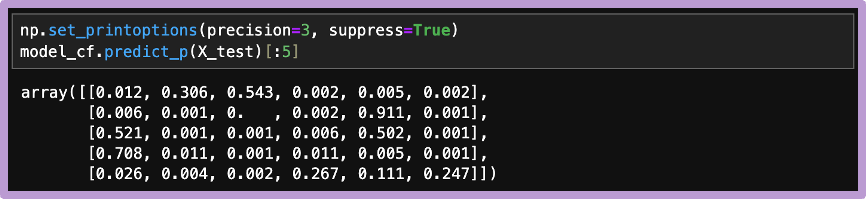
p値は、predict_pメソッドで計算できます。これは各データポイントの各クラスへの適合度でした。この値が大きいほど、低い信頼度の予測集合にも含まれやすくなります。

実際の予測集合の確認には、predict_intメソッドを使います。カバレッジ保証の水準は有意水準αで調整され、この水準以上の箇所に、FLGが立っていることがわかります。

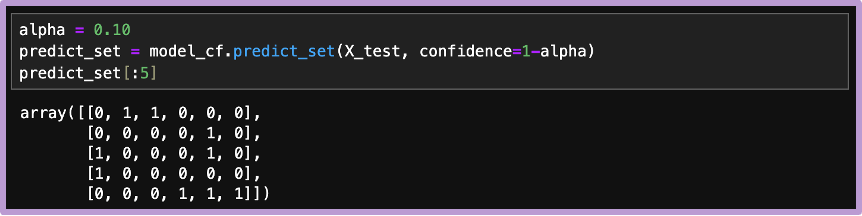
最後に、予測集合に正解ラベルが含まれる割合を確認すると、期待通り、検証データの90%以上で正解ラベルが含まれていることが確認できます。

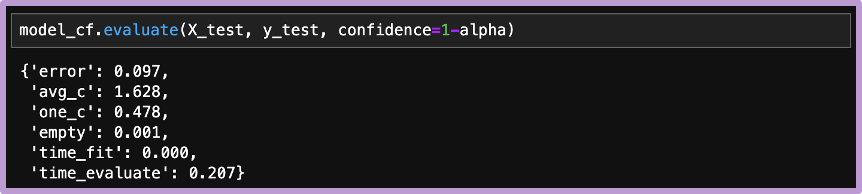
上記結果は、crepesのevaluateメソッドでも確認できます。90.3%の正解ラベルが予測区間に含まれるので、エラー率は 1-0.903=0.097 です（参考：avg_cは予測集合の要素数の平均値、one_cは予測集合の要素数が1の割合、emptyは予測集合が空集合の割合です）。

まとめ

本記事では、コンフォーマル予測が提供してくれるものと、背景にある考え方について紹介しました。特に今回の内容は、コンフォーマル予測の中で最も一般的なもので、専門的には帰納的コンフォーマル予測（Inductive Conformal Prediciton：ICP）と呼ばれます。

ただ、このICPには改善の余地が多いのも事実です。例えば、図４で示した予測区間は等幅であり、これはICPの特徴であり限界です。また、予測集合のカバレッジは、クラス全体での平均的な保証となっており、個別クラスでの保証は提供していません。 

実務では、より精緻な保証が求められることがあるため、分類・回帰の双方に適用可能なMondrian Conformal Prediction（特徴量の部分空間ごとのカバレッジを保証）や、分類に対するClass-Conditional Conformal Prediction（クラスごとのカバレッジを保証）など、より高度な手法については、次回以降に紹介したいと思います。

無料特典のご案内

無料特典登録をしてもらうと、このブログ記事の原稿とPythonサンプルコードを、無料でダウンロードいただけます。