問題意識
予測モデルの精度が高ければ、それで十分と思っていませんか?
AUCやF1スコア、正解率といった分類モデルの評価指標は、モデルの汎化性能を評価するうえで有用です。しかしこれらの指標が良いからといって、ビジネスの現場で最良の意思決定を円滑に下せるとは限りません。
たとえば、営業現場では「どのリードに人的資源を投下するか?」という判断が収益に直結します。このような場面では、単にスコアの高い順に営業するのではなく、「どこまで営業すれば最も利益が出るのか?」という意思決定ルールの設計が求められます。
こうした課題に対し、scikit-learn1.5で登場した TunedThresholdClassifierCV は強力な解決策になります。本記事では、実務でありがちな「受注確率スコアを使ったリードスコアリング」を題材に、利益最大化に効く閾値チューニングの方法と実装例を紹介します。
営業判断時の「閾値設定」の重要性
ある営業チームがWebからの問い合わせや資料請求といったインバウンドのリードに対し、人的リソースを投下すべきかどうかを判断するために予測モデルを導入したとしましょう。
このような場合、リードごとに「受注の可能性があるか否か」を予測する2値分類モデルを構築し、predict_proba() を使って受注確率スコアを算出するのが一般的で、受注確率が高いリードから優先的に営業をかけるという運用になります。
しかし営業資源(特に人による対応)には限りがあり、すべてのリードに対応することは現実的ではありません。このとき重要になるのが、「どの確率を境界にして、営業する/しないを分けるか」という判断です。これは単なるモデル精度の問題ではなく、どのようにリソースを割くと「最も利益が得られるか」という意思決定の問題に他なりません。
TunedThresholdClassifierCVで実現する「利益最適化型の分類」
こうした課題に対して、scikit-learn1.5で新たに追加された TunedThresholdClassifierCV が役立ちます。通常、scikit-learnの分類器のpredict()は、確率スコアが0.5以上かどうかを閾値として分類を行います。
しかし、この「0.5」という値は0と1の単なる中間値にすぎず、ビジネスの現場にとって最適とは限りません。なぜなら、予測ミスにかかる損失は、状況によってまったく異なるからです。
そんなとき、TunedThresholdClassifierCV はモデルの出力確率に対して、どこに閾値を置けばビジネス上の利益が最大化されるかを自動で探索・調整してくれます。つまり、「このスコアを超えたら営業対象にする」というルールを、精度ではなく利益の観点からチューニングしてくれるのです。
利益・コストを定量化して意思決定ルールに落とし込む
TunedThresholdClassifierCV を実際に使うには、「このスコア以上なら営業する」という仮想的な意思決定ルールを前提に、その判断が過去の実績と照らしてどれだけの利益や損失を生むかを評価する必要があります。このために、予測の結果と実際の受注結果がどのように対応していたか(混同行列)をもとに、各パターンにおける「期待される利益/損失」を定義することから始めます。
また、ここでは前提として、以下の条件を置くものとします:
– 予測モデルは、暗黙的なものを含め一次選別を通過したリードに対して構築されている(※1)
– 営業リソースをかけなければ受注は発生しない(※2)
※1:受注ラベルが観測可能な「営業アプローチ済リード」のみ予測モデリング対象となっているという意味です。営業対象外のリードは、受注結果が未観測(欠損)であり、0(失注)として扱うのは誤解を招くため除外します。これは暗黙の足切りによって生じる構造的欠損への対応です。
※2:以下の損益モデルでは、営業活動がなければ契約は成立しないという前提に立ちます(例:完全な法人営業モデルなど)。この前提により、「営業対象から外された場合の逸失利益」を明確に定義できるようになります。もし自然流入や自動継続など、営業を介さずに契約が成立するケースが想定される場合は、その分だけ逸失利益の見積もりを調整する必要があるでしょう。
混同行列ベースで設計する「損益モデル」
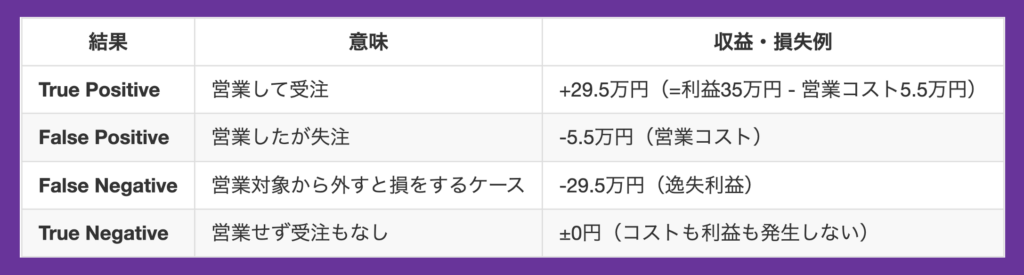
混同行列に基づき、各予測パターンがどのような利益・損失を生むのかを設定します。
このように「当たり/外れ」では捉えきれない損益構造を明確にすることで、「どこで閾値を切るべきか?」という問いに対して、より現実的な解を導くことが可能になります。
実装例:利益を最大化するための閾値チューニング
単に「当たった/外れた」だけでは見えなかった判断の重みを、利益・コストという軸で評価反映できるのが TunedThresholdClassifier の魅力です。続けてこの損益構造を実装に落とし込みながら、実際に scikit-learn 上で最適閾値をチューニングするプロセスを紹介します。
以下で、正例が2割、特徴量が10個の人工データを1000件を作り、閾値調整前の分類器(ロジスティック回帰モデル)の構築と、上記の損益モデルを反映したスコア関数の定義を行います。
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import make_scorer, confusion_matrix
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.sans-serif'] = ['Hiragino Sans', 'Yu Gothic', 'Meiryo', 'Takao', 'IPAexGothic', 'IPAPGothic']
# 1. データ準備(実案件では営業リードの特徴量・受注ラベルに置き換える)
X, y = make_classification(n_samples=10000, n_features=10, weights=[0.8, 0.2], random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=0.2, random_state=0)
# 2. ベースモデルの学習
untuned_model = LogisticRegression(random_state=0)
untuned_model.fit(X_train, y_train)
# 3. 利益・コストの設計(営業活動に合わせて調整)
# 期待利益行列: [TN, FP, FN, TP]
cost_matrix = np.array([0, -55000, -295000, 295000])
# 3. スコア関数の定義(損益をスコアとして使う)
def profit_score(y_true, y_pred):
# >confusion_matrix(np.array([0,0,1,1,1]), np.array([0,0,1,1,1]))
# >array([[2, 0],
# > [0, 3]])
# >confusion_matrix(np.array([0,0,1,1,1]), np.array([0,0,1,1,1])).ravel()
# >array([[2, 0, 0, 3]])
cm = confusion_matrix(y_true, y_pred).ravel()
return np.dot(cost_matrix, cm)
scorer = make_scorer(profit_score, greater_is_better=True)以下は、TunedThresholdClassifierCV を用いて最適な閾値を求める実行コードです。実現利益の確認のため、閾値を1%ずつ変化させた際の利益を、FixedThresholdClassifier (分類器の閾値を外部から直接指定することができるもの)を使って計算しています。
def optimize_and_visualize_threshold(
untuned_model,
X_train,
y_train,
X_test,
y_test,
scorer,
cost_matrix=None,
random_state=0
):
"""
閾値最適化を行い、結果を可視化する関数
Parameters:
-----------
untuned_model : 学習済みの分類器
ベースとなる分類器(閾値を最適化する前のモデル)
X_train : array-like
学習データの特徴量
y_train : array-like
学習データのラベル
X_test : array-like
テストデータの特徴量
y_test : array-like
テストデータのラベル
scorer : callable
スコア関数(利益などの評価指標を計算する関数)
cost_matrix : array-like, optional
コスト行列(利益計算に使用するコスト情報)
random_state : int, default=0
乱数シード
Returns:
--------
tuned_model : TunedThresholdClassifierCV
閾値最適化後のモデル
thresholds : array
評価した閾値の配列
profits : array
各閾値に対応する利益の配列
"""
import matplotlib.gridspec as gridspec
from sklearn.metrics import ConfusionMatrixDisplay
from sklearn.model_selection import StratifiedKFold
from sklearn.model_selection import FixedThresholdClassifier, TunedThresholdClassifierCV
# 異なる閾値での利益をシミュレーション
thresholds = np.linspace(0, 1, 100)
profits = []
# 異なる閾値での利益計算
for threshold in thresholds:
fixed_threshold_model=FixedThresholdClassifier(
estimator=untuned_model,
threshold=threshold
)
profits.append(scorer(fixed_threshold_model, X_test, y_test))
# TunedThresholdClassifierCVの定義と学習
tuned_model = TunedThresholdClassifierCV(
estimator=untuned_model,
cv=StratifiedKFold(n_splits=5, shuffle=True, random_state=random_state),
scoring=scorer
)
tuned_model.fit(X_train, y_train)
# 可視化のためのレイアウト設定
fig = plt.figure(figsize=(15, 12))
# gridspecを使って明示的にサブプロット領域を定義
gs = gridspec.GridSpec(2, 2, height_ratios=[1, 1], width_ratios=[1, 1])
gs.update(hspace=0.2, wspace=0.4) # hspaceを小さくすると上下の間隔調整が可能
# 上段: 閾値と利益のプロット(両列を結合)
ax_top = plt.subplot(gs[0, :])
# 閾値と利益のプロット
ax_top.plot(thresholds, profits)
ax_top.axvline(x=tuned_model.best_threshold_, color='r', linestyle='--',
label=f'tuned threshold: {tuned_model.best_threshold_:.2f}')
ax_top.axvline(x=0.5, color='g', linestyle='--',
label=f'default threshold: 0.5')
ax_top.set_xlabel('Decision Threshold')
ax_top.set_ylabel('Expected Profit')
ax_top.set_title('Optimization of Decision Threshold for Maximum Expected Profit')
ax_top.grid(True)
ax_top.legend()
# 下段左: 最適化済みモデルの混同行列
ax_bottom_left = plt.subplot(gs[1, 0])
disp1 = ConfusionMatrixDisplay.from_estimator(tuned_model, X_test, y_test, ax=ax_bottom_left)
ax_bottom_left.set_title(f'最適化済み閾値({tuned_model.best_threshold_:.2f})モデル')
# 下段右: 未最適化モデルの混同行列
ax_bottom_right = plt.subplot(gs[1, 1])
disp2 = ConfusionMatrixDisplay.from_estimator(untuned_model, X_test, y_test, ax=ax_bottom_right)
ax_bottom_right.set_title('デフォルト閾値(0.5)モデル')
# レイアウト調整
plt.subplots_adjust(top=0.95, bottom=0.05, left=0.1, right=0.9)
plt.show()
# 最適化されたモデルと評価結果を返す
return tuned_model, thresholds, profits
# 閾値最適化と可視化の実行
tuned_model, thresholds, profits = optimize_and_visualize_threshold(
untuned_model=untuned_model,
X_train=X_train,
y_train=y_train,
X_test=X_test,
y_test=y_test,
scorer=scorer,
cost_matrix=cost_matrix
)
# 最適な閾値を確認
print(f"最適な閾値: {tuned_model.best_threshold_:.4f}")
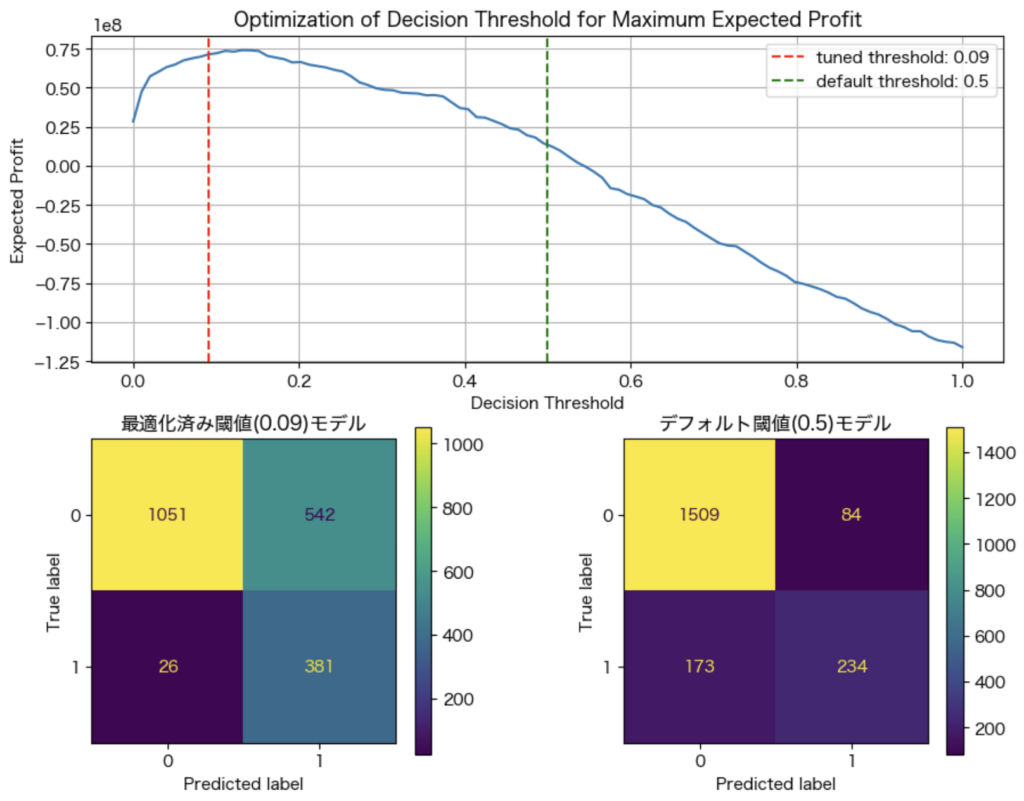
print(f"最適な閾値での利益: {max(profits):.2f}")この実行結果は以下の通りで、最適な閾値は0.09だとわかります。
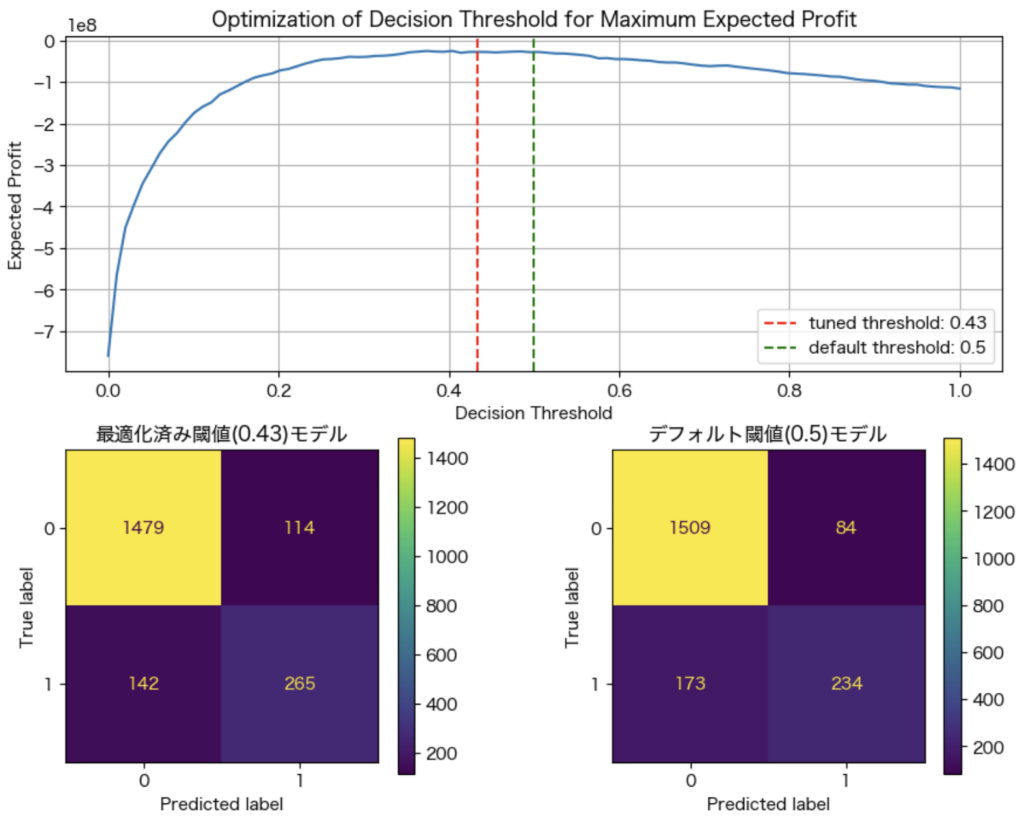
ただ、架空の設定値では実感を伴いにくいため、営業コストを10倍にしたケースも見てみます。利益を変えずコストだけを膨らませたため、False Positiveを抑える方向に結果が変化します。機会損失を許容する代わりに、過大な営業コストが抑制されているという訳です。
# 異なるコスト設定
cost_matrix = np.array([0, -55000*10, -295000, 295000])
# 閾値最適化と可視化
tuned_model, thresholds, profits = optimize_and_visualize_threshold(
untuned_model=untuned_model,
X_train=X_train,
y_train=y_train,
X_test=X_test,
y_test=y_test,
scorer=scorer,
cost_matrix=cost_matrix
)
# 最適な閾値を確認
print(f"最適な閾値: {tuned_model.best_threshold_:.4f}")
print(f"最適な閾値での利益: {max(profits):.2f}")
営業コストが過大になった分、人的資源を投下する閾値が0.09から0.43へと上昇しています。
まとめ:予測を“意思決定”につなげるために
機械学習モデルの精度を高めることは、データ分析の王道です。しかし本当に重要なのは、その予測結果をどう解釈し活用するかです。特に営業のように人という限られた資源をどこに投下するかが利益に直結する場面では、「予測が当たるかどうか」だけではなく、どのような判断が最も利益を生み出すかが重要になります。
今回紹介した TunedThresholdClassifierCV は、こうした文脈で非常に有効なツールです。主なポイントは以下の通りです:
- 予測精度ではなく「ビジネス成果(利益)」を最適化指標にできる
- 営業リソースなどのコストを明示的に判断に組み込める
- モデルと意思決定ルールを分離できるため、現場の変化に柔軟に対応可能
この考え方は、もちろん営業だけにとどまりません。たとえば…
- 採用判断(候補者に面接するかどうか)
- 離反顧客への対応(離反防止のために優先対応をするかどうか)
- 与信管理(どの顧客に融資するか)など
予測に基づき「Yes/Noを決めるすべての意思決定」に応用可能です。重要なのは機械学習モデルをビジネス意思決定の文脈に接続する視点です。精度指標の比較から一歩踏み込み、「その予測がどのような行動をもたらし、どのような結果に繋がるのか?」を定量化しておくことで、機械学習の価値はより現実的で強力なものになるでしょう。
















Comment